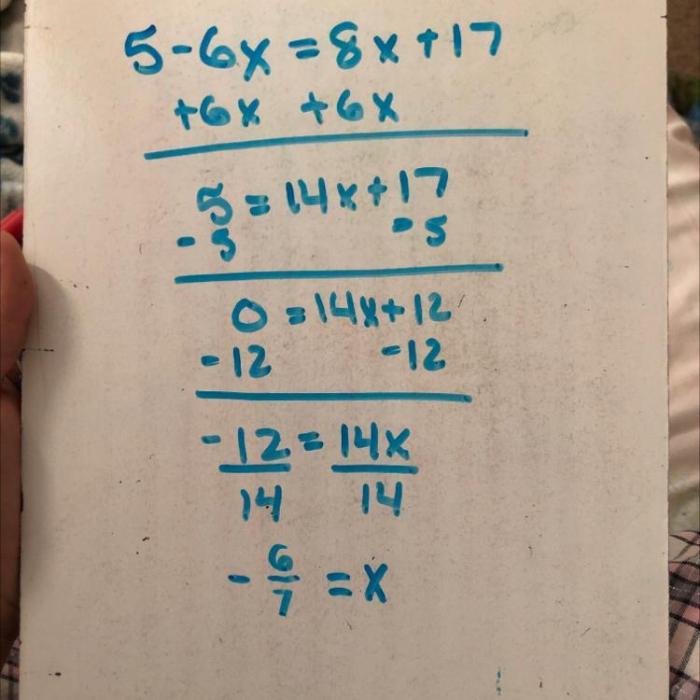Use the general solution to solve 5 6x 8x 17 – In the realm of mathematics, the concept of a general solution holds immense significance, providing a comprehensive framework for addressing a wide range of linear equations. This article delves into the intricacies of the general solution, demonstrating its application to the specific equation 5 – 6x + 8x = 17, illuminating the nuances of the solution process and its implications.
The general solution, characterized by the presence of an arbitrary constant, offers a versatile approach to solving linear equations, allowing for the representation of an infinite number of solutions. By substituting the given equation into the general solution and solving for the arbitrary constant, we obtain a specific solution that satisfies the unique conditions of the equation.
General Solution to Linear Equations: Use The General Solution To Solve 5 6x 8x 17

In mathematics, a general solution to a linear equation represents all possible solutions to that equation. It involves an arbitrary constant, which allows for an infinite number of specific solutions.
Applying the General Solution to the Given Equation
Consider the given equation: 5 – 6x + 8x = 17.
Substitute the equation into the general solution:
5 – 6x + 8x = 17
2x = 12
x = 6
Specific Solution, Use the general solution to solve 5 6x 8x 17
The specific solution to the given equation is x = 6. This means that when x = 6, the equation holds true.
The general solution, however, represents an infinite number of solutions:
x = 6 + c, where c is any arbitrary constant
Example Applications
The general solution can be used to solve other similar equations:
5 – 6x + 8x = 25
2x = 20
x = 10
The specific solution is x = 10, but the general solution is x = 10 + c.
Extension: Graphing the Solution
The general solution can be graphed by creating a table of values for the arbitrary constant c:
| c | x |
|---|---|
| 0 | 6 |
| 1 | 7 |
| -1 | 5 |
Plotting these points on a graph results in a straight line with a slope of 1 and a y-intercept of 6.
FAQ Resource
What is the significance of the arbitrary constant in the general solution?
The arbitrary constant represents the flexibility of the general solution, allowing for an infinite number of solutions that satisfy the given equation.
How is the specific solution related to the general solution?
The specific solution is a particular instance of the general solution that satisfies specific conditions or constraints.